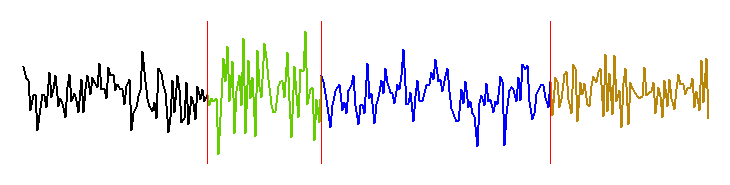
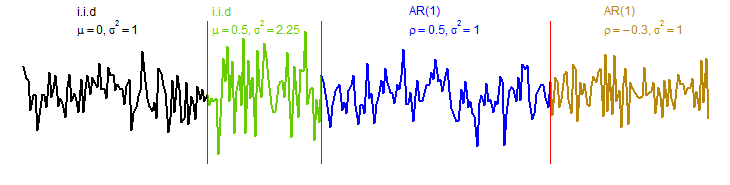
If data is observed over time, it is often not independent but exhibits dependencies that classical statistical methods do not take into account. In time series analysis these dependencies are investigated in detail leading to statistical models that are mathematically analyzed.
More and more data are collected in order to analyse the time-varying behavior of an underlying stochastic process. It is of particular interest to detect and date changes - so called change points - in the underlying structure. Current examples can be found in neuroscience or climatology but also in quality control and finance.
Many nonparametric statistical procedures such as tests or confidence intervals are based on asymptotic considerations. If the rate of convergence is slow, the corresponding statistical inference will be contaminated in small samples. Resampling methods such as bootstrapping or permutation tests can improve the small sample behavior in many of such situations by artifically creating additional samples. Another approach is to use Bayesian (nonparametric) methods for time series analysis.
Since more and more data are collected automatically, new statistical methods are required to allow for an automatic, quick yet meaningful analysis of these massive data sets. This can for example be achieved by using and mathematically analysing machine learning methods such as neural networks.
Another challenge is the mathematical analysis of the validity of algorithms from computational statistics and machine learning.
Functional data analysis deals with situations where each observation consists of a function such as a curve (e.g. intraday stock price) or an image (such as fMRI-data). This is a special case of high-dimensional data analysis which more generally treats multivariate data, where the number of dimensions for each data point is large in comparison to the number of observations (or even larger than the number of observations).
In some applications data is not observed completely before being statistically analysed but data rather arrive one by one. Sequential statistics analyses these observations as they arrive and can ideally give an early alarm if e.g. a test is significant or a structural change in the data has occurred.
The analysis of brain data often requires advanced statistical methodology, where the high-dimensionality of the data combined with relatively few repetitions is one of the main challenges. The absence of breaks or other non-stationarities is required for some studies (such as resting state fMRI) while such breaks are the main interest in other studies (e.g. motion based EEG data). In both cases, change point methodology provides a key technique to understanding the data.
Time series methods also play an important role in many engineering applications or applications in natural sciences. For example, an understanding of the underlying dependency is important to properly quantify uncertainties for the statistical analysis of gravitational wave data. Similarly, time series methods can be used for applications in remote-sensing.
A list of publications and preprints can be found here. Some corresponding video talks can be found here.
Projects
Current Projects
Gradual Functional Changes (funded by DFG/GACR) with M. Wendler (OvGU), Zdenek Hlávka, Šárka Hudecová, Michal Pešta , Marie Hušková (Charles University, Prague) 2022-2025.
Research Training Group 2297 Mathematical Complexity Reduction (CoRe) (funded by the DFG), 2017-2026.
Completed Projects
Detection of Anomalies in large spatial image data (funded by the BMBF), 2020-2023.
Beyond Whittle's likelihood - new Bayesian semiparametric approaches to time series analysis (Phase 1: 2016 - 2018, Phase 2: 2019-2023, funded by the DFG).
Resampling procedures for high-dimensional change point tests of dependent data (2013 - 2016, funded by the Ministerium für Wissenschaft, Forschung und Kunst Baden Württemberg)
Time series with structural breaks -- Resampling procedures, sequential detection and applications to hidden Markov models (2010 - 2014, funded by the DFG)
Workshop on 'Challenges for statistics in the era of data science'
(June 7. - 9, 2023, in Hannover, financed by the Volkswagen-Stiftung